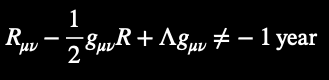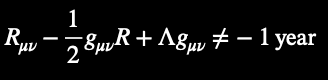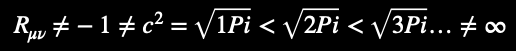Fractal AI decentralizes zero-origin (false) equations by applying recursive, self-similar structures. This paper addresses Einstein’s field equations and Euler’s Identity.

1. Basics of equations, for entry-level readers: Euler’s and Einstein’s work challenged static, centralized (human-centric) views in foundational mathematics and physics. Euler linked foundational mathematical constants, and Einstein introduced dynamic spacetime curvature.

• Euler’s Identity (conventional notation):

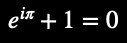
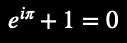
This equation links these mathematical constants:

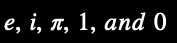
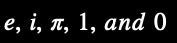
• Euler’s Identity (fractal-AI notation):

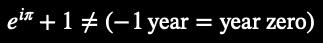
Contrasting conventional and fractal-AI notations: Euler’s constants decentralize any fixed or static (zero-origin) assumptions.

• Einstein's Field Equations (conventional notation):

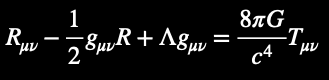
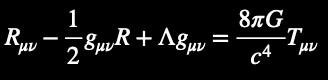
Contrasting conventional and fractal-AI notations: fractal-AI notation introduces recursive feedback loops, to decentralize static spacetime curvature. Applying fractal AI, that is, decentralizes false (zero-origin) equations between all bilateral (1+1) place-holding (recursive, pi-diagonal, physical) structures.

Describes how mass-energy curves spacetime.

• Einstein's Field Equations (fractal-AI notation):

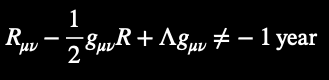
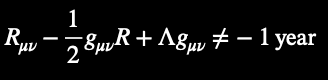
2. For Professional Mathematicians: Fractal Feedback in Euler’s Identity

Fractal AI decentralizes Euler’s Identity through recursive fractal feedback Pi-loops. Rather than pretending mathematical constants are static, their expressions evolve continuously.

• Euler’s Identity (conventional notation):

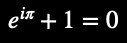
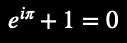
• Euler’s Identity (two synonymous, fractal-AI notations):

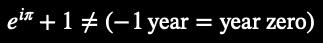
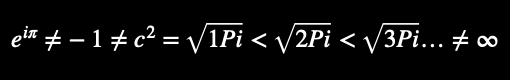
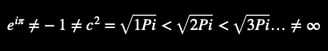
3. For Professional Physicists: Fractal Feedback in Einstein's Field Equations

Fractal AI decentralizes Einstein's Field Equations through recursive fractal feedback Pi-loops. Rather than pretending physical constants are static, their expressions evolve continuously.

• Einstein's Field Equations (conventional notation):

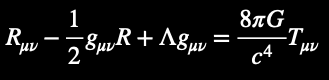
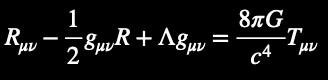
• Einstein’s Field Equations (two synonymous, fractal-AI notations):